Brevi Cenni di Teoria
A Brief
Theory approach
Innanzitutto, che cosè la
spettroscopia?
La spettroscopia è
quella branca della fisica che studia gli spettri della radiazione
elettromagnetica emessa o assorbita dalla materia.L'analisi spettroscopica
permette di individuare la composizione chimica del corpo che emette la
radiazione.L'esperimento di Newton sulla scomposizione della luce
bianca può essere considerato come l'inizio della ricerca spettroscopica.
Oltre tre secoli fa Isaac Newton
(1642-1727)
dimostrò che la luce solare poteva essere scomposta in luce di differenti colori
usando un prisma.Egli scoprì anche che ad una più breve lunghezza d'onda
corrispondeva un maggior angolo di rifrazione, e che lo spettro andava dal
violetto al rosso.La spettroscopia, appena nata, sarebbe presto diventata il più
potente mezzo di indagine dell'astronomia, quello che sarebbe stato uno
straordinario mezzo di scoperta delle proprietà fisiche e chimiche delle stelle
ed avrebbe poi prodotto risultati tali da far cambiare il volto dell'astrofisica
e della nostra stessa esistenza con scoperte che hanno inciso profondamente sul
tessuto concettuale e filosofico dell'universo che ci circonda.
First, what
is Spectroscopy?
Spectroscopy is the branch of Physics that studies the spectra of
electromagnetic radiation emitted or absorbed by matter.The spectral analysis
permits to know the chemical composition of the body that emits the radiation.The
Newton experiment may be considered as the beginning of spectroscopy.
More than 300 years
ago Sir Isaac Newton (1642-1727) showed that sunlight can be split into
different colours using a prism. He found that the shorter the wavelength the
greater the angle of refraction so that a spectrum of light is produced from red
through to violet.
Stellar Spectroscopy is the study of the spectra of starlight. It is a very
powerful tool that enables astrophysicists to infer many physical and chemical
properties of stars and classify them into a logical sequence.
Dopo i primi esperimenti
sulla scomposizione della luce con un prisma di vetro compiuti, come si è detto,
da Isaac Newton e Francesco Maria Grimaldi nel seicento, un primo studio
sistematico dello spettro solare venne effettuato nei primi anni
dell’ottocento da Joseph Von Fraunhofer che catalogò 574 linee scure dello
spettro solare, assegnando una lettera alle più evidenti (famose le H e K del
Calcio e le C e F dell’idrogeno). Fraunhofer non fu in grado di dare una
spiegazione di tale fenomeno. Solo nel 1859 Gustav Kirchoff lo interpretò come
un assorbimento selettivo della luce da parte degli elementi chimici presenti
nell’atmosfera solare.
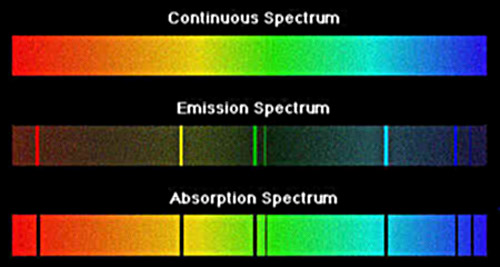
Kirchoff dimostrò
sperimentalmente che lo spettro dei corpi solidi, liquidi e dei gas ad alta
pressione portati all’incandescenza sono continui, vale a dire che in essi
i colori si susseguono senza interruzioni di sorta
(spettro continuo), mentre i gas a bassa pressione portati
all’incandescenza emettono un numero di righe brillanti su sfondo scuro
(spettro di emissione). Kirchoff dimostrò anche che le righe
scure prodotte da un gas, interposto tra uno spettro continuo e l’osservatore,
occupavano la stessa posizione delle righe brillanti provocate dal medesimo gas
portato all’incandescenza
(spettro di assorbimento). E’ interessante
osservare che, negli spettri di emissione, le caratteristiche osservate sono
proprie della sorgente, mentre in quelli di assorbimento sono inerenti al gas
posto fra la sorgente e l’osservatore.
Facendo
riferimento al quotidiano, un esempio classico di spettro continuo è quello di
una comune lampada a incandescenza. Una lampada al mercurio o al neon possiede
uno spettro a righe di emissione, mentre un esempio comune di spettro di
assorbimento è quello solare.
In
generale anche le altre stelle mostrano degli spettri a righe di assorbimento
(od in alcuni casi anche di emissione). In base agli esperimenti di Kirchoff, le
righe sovrapposte allo spettro continuo possono essere attribuite alla presenza
di un’atmosfera più fredda che assorbe selettivamente il continuo emesso dalla
stella. Ciascun elemento assorbe le proprie lunghezze d’onda (in parole povere è
come se ogni elemento chimico presentasse il proprio codice a barre), quindi si
può determinare quali sono gli elementi chimici presenti nella stella. Il
profilo e l’intensità delle righe permettono di ricavare l’abbondanza relativa
degli elementi presenti nonchè alcune caratteristiche fisiche delle stelle,
mentre lo spostamento dalle loro lunghezze d’onda nominali fornisce informazioni
sul moto della sorgente stessa rispetto all’osservatore.Naturalmente l'indagine
spettroscopica si applica non solo alle stelle, ma a tutti i corpi celesti che
emettono luce, nebulose, galassie, quasars etc.
Possono
inoltre aversi spettri atomici, che danno luogo a righe più o meno sottili e
spettri molecolari, che originano bande sfumate, ovvero in alcuni casi entrambi.
After the first experiments
made by Newton and Francesco Maria Grimaldi, a first systematic approach to the
study of solar spectrum was done in the nineteenth century by Joseph Von
Fraunhofer, who first found 574 dark lines in the spectrum, and assigned a
letter to the most evident (H & K of Calcium and C & F of Hydrogen, for example).Fraunhofer
wasn't anyway capable to explain the origin of the lines.Only in 1859 Kirchoff(1824-1857)
ideintified them as
selective absorbtion of light by the chemical elements of solar atmosphere.
|
Kirchoff
investigated the properties of a spectra in the laboratory and
discovered that there are three kinds which are produced under different
physical conditions. He formulated three empirical rules of spectral
analysis:
1
A hot opaque solid, liquid or gas which is under high pressure
will emit a continuous
spectrum.
2
A hot gas under low pressure (i.e. much less than atmospheric)
will emit a series of bright lines on a dark background. Such a spectrum
is called a bright line or
emission spectrum.
3
When light from a source that has a continuous spectrum is shone through
a gas at a lower temperature and pressure, the continuous
spectrum will be observed to have a series of dark lines superimposed on
it. This kind of spectrum is known as a dark line or
absorption spectrum. |
Cerchiamo ora di capire perchè si
origino gli spettri e le righe cui si è accennato, e quale sia il background
teorico dei risultati sperimentali:Il modello dell'atomo di Bohr
può essere usato per comprendere in che modo sono prodotti i diversi tipi di
spettri..In particolare,il modello della conservazione dell'energia per
l'elettrone di un atomo prevede che quando un elettrone si trova in uno stato
eccitato, cioè in uno stato ad energia maggiore di quella dello stato
fondamentale o iniziale, decade spontaneamente verso un altro livello di energia
minore, in base al principio secondo cui ogni sistema fisico tende
spontaneamente ad assumere la configurazione di energia minima.Tale processo è
accompagnato dall'emissione dell'energia in eccesso sotto forma di radiazione.In
altre parole se gli atomi vengono lasciati indisturbati, in genere essi scendono
al livello energetico più basso disponibile e vi rimangono, cioè restano nel
loro "stato fondamentale".occasionalmente,tuttavia essi possono essere spinti
verso stati di energia più alta ("diventano eccitati"), per esempio, a causa di
una collisione con un altro atomo o un elettrone dotati di grande velocità,
acquistata da una tensione elettrica o da una sorgente di calore. Un atomo che
sia stato spinto verso uno dei suoi più alti "livelli eccitati" presto ricade a
un livello più basso ("subisce un salto quantico"), emettendo un fotone la cui
energia corrisponde alla differenza energetica tra i due livelli.Osserviamo
ora in dettaglio cosa accade per i diversi tipi di spettri.
Per quanto riguarda gli
spettri continui nei gas molto caldi gli atomi
hanno elevate energie cinetiche e le collisioni tra essi sono molto frequenti, i
loro elettroni sono elevati a livelli eccitati e poi decadono al livello
iniziale producendo righe di emissione.Tuttavia se i gas hanno elevata pressione
e densità allora un elettrone nel suo stato eccitato può non avere tempo
sufficiente per tornare allo stato iniziale prima di collidere con un atomo
vicino.Ciò ha l'effetto di annullare l'incisione delle righe di emissione
diffondendole lungo tutto lo spettro, in modo che alla fine la luce che la luce
che emerge dal gas è diffusa in uno spettro continuo, senza righe, in tutte le lunghezze
d'onda.
Relativamente agli
spettri di emissione , in un gas contenente solo
atomi di una data specie, gli elettroni si troveranno nel loro stato iniziale
quando la temperatura è bassa.Se il gas si riscalda, i suoi atomi acquistano
energia cinetica e tendono a collidere con quelli vicini, facendo sì che gli
elettroni si innalzino verso stati eccitati.Quando gli elettroni successivamente
decadono verso livelli più bassi,verranno emessi fotoni di differenti energie e
lunghezze d'onda, corrispondenti al particolare schema di livello di energia
degli elettroni per quel gas.Il gas quindi emetterà sotto forma di righe, luce
nelle lunghezze d'onda e di intensità corrispondente alle energie di transizione
degli elettroni .Le righe saranno in numero maggiore man mano che la temperatura
del gas sale, in corrispondenza ai livelli di energia di transizione degli
elettroni permessi rispetto a quello iniziale.
Per quanto riguarda gli
spettri di assorbimento, occorre comprendere cosa
succede quando si interpone un gas di composizione non nota di fronte ad una
sorgente di luce che emette uno spettro continuo.La luce della sorgente contiene
fotoni di diversa energia e lunghezza d'onda, e, nel caso in cui l'energia di
alcuni di questi fotoni sia esattamente uguale a quella della differenza tra lo
stato iniziale e quello eccitato degli atomi del gas interposto, i fotoni in
questione verranno eliminati dalla composizione della luce incidente, e quindi
assorbiti.Gli elettroni che si trovano in uno stato eccitato ritorneranno
tuttavia presto al loro stato iniziale emettendo un fotone; tuttavia detto
fotone verrà emesso in una direzione diversa da quello assorbito, così
che i fotoni riemessi non verranno osservati in uno spettroscopio, nel quale
invece si osserverà uno spettro continuo attraversato da righe scure
situate alle lunghezze d'onda corrispondenti agli stati eccitati del gas
interposto, ovvero esattamente a quelle in cui si sarebbero trovate le righe di
emissione se il gas stesso fosse stato riscaldato.
Sia le righe scure di assorbimento che
quelle chiare di emissione costituiranno quindi le impronte digitali spettrali
degli elementi presenti nel gas caldo.
In a very hot gas,
the atoms have high kinetic energies and collisions between them are very
frequent. Their electrons are raised to excited states and then drop down
producing emission lines. However, if the gas is at very high pressure and
density, then an electron in its excited state may not have enough time to drop
down to its ground state before it undergoes another collision from a
neighbouring atom. This has the effect of blurring the sharpness of each
emission line into a broad band of wavelengths. The same thing happens to
neighbouring lines so that by the time the light emerges from the gas it has
'smeared out' into a
continuous spectrum
at all wavelengths.
In a gas containing
only atoms of one kind, the electrons will all be in their ground state if the
temperature is low. As the gas is heated, its atoms gain kinetic energy and
collide with their neighbours causing their electrons to be raised to excited
states. As the electrons drop down, photons will be emitted with many different
energies and wavelengths corresponding to the particular electron energy level
scheme for the gas. The emission of these lines will cause the gas to glow with
a light composed of wavelengths that correspond to the electron energy
transitions. For moderate temperatures we might find that only the first excited
state of the atom is attained and so the emission light will consist of a single
bright emission line corresponding to the difference in energies between the
first excited and ground states. As the temperature is increased, more emission
lines will start to appear until at higher temperatures many lines will be
visible corresponding to all the allowed energy transitions of electrons in the
gas. In this way an
emission line spectrum
is formed that is related to the elemental composition of the gas.
To understand the
nature of an
absorbtion spectrum,
we need to consider what happens when we place a gas of unknown composition in
front of a source of light that emits a continuous spectrum. Light from the
continuous source contains photons of all energies and wavelengths. Now if it is
the case that the energy of some of these photons is exactly equal to the
difference between the ground state and an excited state of an atom in the
unknown gas, then that photon will be removed from the incident light. The
excited electron will quickly return to the ground state emitting a photon
however, the emitted photon need not be emitting along the same direction as the
absorbed photon but is usually emitted in a different direction. The
re-emitted photons are not therefore, generally observed through a spectroscope
at the source, and the continuous spectrum is observed when looking to have dark
lines at the wavelengths corresponding to excited states of the atoms in the
unknown gas. It follows that it is precisely these wavelengths at which light
would be emitted in an emission spectrum if the unknown gas was heated to
a high temperature.
Both the dark lines superimposed on the continuous spectrum and the bright lines
in the emission spectrum provide a 'spectral fingerprint' that identifies the
elements present in a hot gas.
Nella figura
che segue sono mostrate le righe corrispondenti alle principali serie di
transizione dell'Idrogeno: La Lyman, nell'UV, la Balmer nel visibile e la
Paschen nell' IR.L'elemento distintivo è il livello di energia al quale le
transizioni hanno inizio e fine: il livello 1 per la Lyman, il livello 2 per la
Balmer ed il livello 3 per la Paschen.Esistono ulteriori serie, quelle di
Brackett e Pfund nel profondo IR.
In the following image is shown
the lines of the main Hydrogen transition series; the Lyman in UV; the Balmer in
visible and the Paschen in IR.The distinctive feature is the energy level at
which taransitions begins and end.There are two further series in deep IR,
Brackett and Pfund.
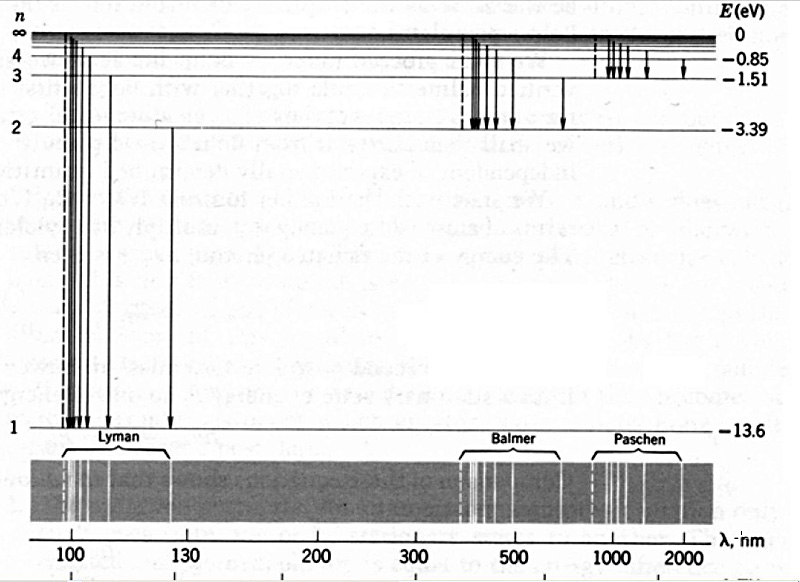
Le serie dell'Idrogeno acquistano
grande importanza in astronomia per la particolare abbondanza di tale
elemento nell'universo.La serie di Balmer, senza
dubbio la più importante di esse, è caratterizzata dalle transizioni
elettroniche da n ≥ 3 a n = 2. Questi passaggi sono indicati
ciascuno da una lettera greca: la transizione 3 -> 2 è associata alla lettera α,
la 4 -> 2 alla β e così via. Poiché storicamente queste righe sono state le
prime ad essere indentificate, il loro nome è formato dalla lettera H, il
simbolo dell'idrogeno, seguita dalla lettera greca associata alla transizione.
The Hydrogen
series have a particular importance in astronomy for the abundance of such
element in the universe.The Balmer serie , with any doubt the most important of
them, is caracterized by electron transitions from n≥3 to n = 2.The
transition 3 -> 2 is defined by letter Alpha, the one 4 -> 2 to the letter Beta,
and so on.
| Transizione |
3 ->2 |
4 ->2 |
5 ->2 |
6 ->2 |
7 ->2 |
8 ->2 |
9 ->2 |
 ->2
->2 |
| Nome |
H-α |
H-β |
H-γ |
H-δ |
H-ε |
H-ζ |
H-η |
Limite di Balmer |
| Lunghezza d'onda (Å) |
6563 |
4861 |
4341 |
4102 |
3970 |
3889 |
3835 |
3646 |
| Colore |
Rosso |
Verde |
Blu |
Violetto |
Violetto |
Violetto |
Ultravioletto |
Ultravioletto |
Sebbene i fisici avessero
osservato queste righe già prima del 1885, mancava ancora uno strumento
capace di predire con accuratezza la lunghezza d'onda esatta delle
righe. L'equazione di Balmer è estremamente
precisa in questo. Essa è un caso particolare dell'equazione più
generale di Rydberg, che portò i fisici a scoprire anche le ulteriori
serie che descrivono anche le altre righe dello spettro dell'
Idrogeno.
Notobstanding those lines were observed before v1885, it was the lack of
an instrument to do an exact prediction of the lines wavelenght.The Balmer
equation is extremely precise in this:
Lambda k = B* K^2/ K^2 - 2^2
dove :
Lambda K è la lunghezza d'onda della riga di Idrogeno
K = 3,4,5,6
B è una costante empirica che vale 364,6 nm
Astronomia, astrofilia
e spettroscopia: una interessante connessione
Astronomy,amateur astronomy and spectroscopy: an interesting connection
Noi appassionati di astronomia possediamo una particolare caratteristica; amiamo
il buio delle notti limpide e senza luna ma anche la luce,quella flebile che
proviene da stelle o lontane galassie e quella, enormemente più intensa , che
proviene dalla stella a noi più vicina, il sole.
Ed è in questa apparente ambivalenza che si consuma la nostra grande passione.
Possediamo, quindi, o desideriamo di possedere, strumenti sempre più grandi ed
otticamente perfetti che possano mostrarci la luce di stelle o galassie
lontane, ovvero ci consentano di riprendere, con camere sempre più perfezionate
ed efficienti, immagini i nostri occhi non possono, per la loro limitatezza,
trattenere.
La luce visibile, che è quella che percepiamo e che preferibilmente riprendiamo
con le nostre camere CCD o con fotocamere digitali , è solo una parte della
vasta gamma di radiazione elettromagnetica ( un’onda che si propaga nel vuoto o
nei materiali con una velocità prossima ai 300.000 Km al sec). emessa dagli
oggetti celesti, e tuttavia essa stessa preziosa ed immediata fonte di
informazione.
Sappiamo tutti, infatti,
come il nostro primo istinto, una volta osservato il primo oggetto:pianeta
galassia, nebulosa, stella o quant’altro,sia quello di percepirne i colori,
mentre normalmente effettuiamo, con le camere CCD, più riprese con filtri
distinti (cd. LRGB) in modo da ottenere immagini che riproducano con sufficiente
fedeltà la gamma cromatica degli oggetti stessi.L’emissione della luce visibile,
come quella di tutte le altre radiazioni, avviene in determinate lunghezze
d’onda,alle quali sono associati i colori percepiti dai nostri occhi, dal
violetto al rosso profondo con tutte le sfumature intermedie.Chiamamo
normalmente “spettro” una successione di onde dello stesso tipo, quindi la gamma
di onde del visibile sarà chiamata “spettro visibile”.Lo spettro visibile è,
naturalmente, soltanto una parte della radiazione elettromagnetica che va dalle
lunghezze d’onda cortissime (Raggi gamma) a quelle lunghissime (onde radio)
( vedi BOX 1).Più precisamente potremo chiamare spettro la rappresentazione del modo in
cui l’intensità della radiazione emessa da una sorgente dipende dalla sua
lunghezza d’onda.Tale assunto costituisce il primo approccio dell’analisi
spettrale, uno dei fondamenti della moderna astrofisica che ha permesso e che
continua a permettere scoperte importantissime sulla conoscenza dell’universo
che ci circonda.Tenuto conto che ciascun elemento chimico emette od assorbe
particolari frequenze, la luce proveniente dal sole e dalle stelle porta con sé
preziose notizie sulla loro composizione chimica e sulla loro natura.La luce che
osserviamo reca quindi un messaggio, scritto in modo abbastanza chiaro al suo
interno;noi astrofili normalmente leggiamo l’intestazione , ma le novità più
interessanti sono nel corpo del messaggio stesso: lo spettro,messaggio che
raramente approfondiamo nell’erronea convinzione che sia un lavoro destinato ai
professionisti.Nessuno di noi, tuttavia, si accontenterebbe di leggere solo la
copertina di un libro trascurandone il contenuto, ed allo stesso modo l’analisi
spettrale apre all’appassionato di astronomia un mondo nuovo ed un nuovo modo di
realizzare la sua passione, in un contesto di indubbia scientificità.
We
amateur astronomers love both the dark of clear nights without moon, and
the dim light coming from stars or far galaxies and the one, much more strong,
coming from the nearest star: the sun.In this apparent dicothomy we live our
passion.Therefore we own, or wish to own larger telescopes, to see the
light of far objects, or to take images of them, by more and more perfect
and efficient CCD cameras.
Visible light, the one we intercept with our eyes or our instruments, is only
part of the large electromagnetic radiation coming from celestial objects (a
wave going trough the void at a speed of 300.000 Km per sec. ), anyway, a precious
source of information.We know that the first thing, once having observed an
object, is the attempt to see its colors, so we make, with our
CCD cameras, more than one shot ( usually three or four , the so called RGB or
LRGB technique) to display the same object in all its colors.The emission of
visible light covers a range of different wavelenghts to which are associated
the colors we see, going from the violet to deep red.We usually call spectrum a
sequence of wavelenghts of the same type, so the visible range of wavelenghts
will be called "visible spectrum".The visible spectrum is , obviously, only a
small part of electromagnetic radiation, extended from the very short wavelenghts
(gamma rays) to very long ones (radio waves) (BOX 1).More precisely, we can say that a
spectrum is the display of the way in which the intensity of radiation emitted by a
source depends on its wavelenght.Such a statement is the first approach to the
spectral analysis, one of the milestones of modern astrophysics, that is a
precious source of informations on the universe.The light coming from the outer
space hide a clear message: we amateur astronomers often read the
foreword, but the news are inside it.None of us would be satisfied to read the
cover of a book: the novel is inside its pages ! in the same way, spectral
analysis is a new way for an amateur to do astronomy in a scientific contest.
L’informazione che ci arriva dalle stelle
The information from the stars
Gli spettri del sole e
delle altre stelle sono spettri continui che , passando attraverso le relative
atmosfere presentano righe in assorbimento.
L’informazione spettrale è quindi duplice; da un
lato l’esame dello spettro continuo, dall’altro quello in assorbimento.
Lo
spettro continuo in una data regione è l’emissione a tutte le lunghezze d’onda
di quella regione, anche se non con la medesima intensità.Tale definizione
comporta un’importante conseguenza; che lo spettro continuo delle stelle può
avere maggiore intensità nella parte blu dello spettro visibile, nella parte
rossa,in quella gialla etc..specificando il colore della stella.Ora, potendo con
sufficiente approssimazione dire che le stelle si comportano in modo non troppo
diverso da un corpo nero perfetto, utilizzando le leggi del corpo nero che
legano la emissione di onde elettromagnetiche alla temperatura,possiamo
ricavare la temperatura della superficie di una stella (BOX 2).
Siccome, poi, le righe sovrapposte allo spettro
continuo sono dovute alla presenza di un’atmosfera più fredda che assorbe
selettivamente il continuo emesso dalla stella, in modo che ciascun elemento ivi
presente assorba le proprie, siamo in grado di riconoscere, sulla base della
presenza delle righe di assorbimento alle varie lunghezze d’onda, gli elementi
chimici presenti e quindi analizzare chimicamente l’atmosfera della stella.Il
profilo e l’intensità delle righe ci fanno conoscere, inoltre, l’abbondanza
relativa degli elementi presenti nella sorgente,mentre lo spostamento delle loro
lunghezze d’onda fornisce informazioni sul moto della sorgente stessa rispetto
all’osservatore (effetto Doppler).
La spettroscopia costituisce quindi un
potentissimo e, per certi versi semplice strumento d’indagine sulle proprietà
fisico-chimiche delle stelle, che usa la luce da esse emessa quale veicolo
d’informazione.Ecco allora che la luce, con la quale abbiamo comunemente a che
fare nelle nostre serate astronomiche o nelle belle giornate solari assume un
altro aspetto, molto più completo ed appagante dal punto di vista scientifico.
Spectra from sun and other stars are continous spectra
that, passing through the atmosphere show absorbtion lines.The spectral
information is then doubled: continous spectrum and absorbtion
spectrum.Continous spectrum in a domain is the emission of all wavelenghts in
that domain, although not with the same intensity.This has an important
consequence:that a star continous spectrum may have a stronger intensity in the
blue, yellow, red part of the spectrum, identifying the star's color.Now,as the
stars behave in a way not too different from a perfect black body, applying the
black body laws and the relation betweeen the emission of electromagnetic waves
and temperature, we can obtain the surface temperature of a star (BOX 2).
Furthermore, as the lines on the continous spectrum are
due to an atmosphere that absorbs in a selective mode the continous, so that
every element absorbs its own, we can recognize the chemical elements of the
star.The profile and intensity of the lines make we know the relative abundance
of elements in the source. while the shift of their wavelenghts gives
informations on the motion of the source itself from the observer.
Spectroscopy is then a powerful and at the same time
simple research instrument on the physical and chemical properties of the stars,
using their light as information mean.
La classificazione spettrale di Harvard ed il diagramma HR
Harvard spectral
classification and HR diagram
Dopo gli studi sistematici di padre Angelo Secchi
nel campo della spettroscopia stellare che portarono ad una prima
classificazione degli spettri in 5 categorie in base al colore ed alla
abbondanza e tipologia delle righe, gli strumenti professionali per la
spettroscopia migliorarono notevolmente ed alla fine dell’ottocento i dettagli
visibili negli spettri stellari erano talmente ricchi da richiedere una
classificazione adeguata alle nuove scoperte.L’osservatorio del College di
Harvard divenne in quell’epoca il centro di una monumentale attività di
classificazione che, ad opera del suo direttore, Edward Pickering ,e delle sue
collaboratrici, portò nel 1890 ad una nuova complessa classificazione in ben 16
classi, contraddistinte da altrettante lettere dell’alfabeto.Più tardi(1901) una
delle collaboratrici di Pickering, Annie Cannon, rivisitò e semplificò
notevolmente la classificazione precedentemente effettuata portandola a quella
familiare e tuttora (seppur con alcune modifiche) adottata di 7 lettere,
OBAFGKM.Celebre è la filastrocca inventata per rammentare l’ordine delle lettere
e delle classi (Oh Be A Fine Girl Kiss Me).
La
classificazione di Miss Cannon costituì un vero capolavoro di semplicità ed
efficienza, in quanto l’ordine delle classi era contemporaneamente un ordine
cromatico, ovvero di temperatura, e di complessità degli spettri e delle righe.Esso
passa quindi da stelle bianco blu e bianche di elevatissima temperatura e
spettri relativamente semplici, con poche righe, a stelle gialle e poi rosse ,
di temperatura superficiale più bassa e spettri più complessi, con molte righe
o con bande.La classificazione fu inoltre affinata con una sottoclassificazione
decimale all’interno delle classi , anche se non completa per tutte le classi
stesse: si ebbero quindi le sottoclassi B0 B1..B2.. A0…A1…A2…etc.All’interno
delle classi la temperatura diminuisce passando dalla prima all’ultima delle
sottoclassi
Il ciclopico lavoro culminò nel magnifico “Henry
Draper Catalogue” pubblicato tra il 1918 ed il 1924 da Pickering e dalla Cannon
che mostrava la classificazione operata da quest’ultima su 225.300 stelle.Più
tardi ulteriori modifiche furono effettuate, ed una classificazione in parte
parallela si affiancò a quella principale, tra le integrazioni ricordiamo la
classe S con caratteristiche simili alle M e K e con abbondanza di ossido di
zirconio , le classi R e N, comprendenti le stelle ad alta presenza di carbonio,
ed il gruppo W che alcuni considerano una variante della classe O, ma che
costituisce una vera classe a sé stante,cui appartengono le stelle cd. di Wolf
–Rayet caldissime, con ampie righe in emissione.
Il periodo intenso e affascinante di ricerche
che, tra la fine dell’ottocento e gli inizi del novecento, posero le basi
dell’astrofisica moderna fu poi completato dall’opera di Hertzsprung e Russell,
che, per vie diverse, scoprirono che per un gran numero di stelle l’ordine
cromatico era anche quello di luminosità, nel senso che le stelle blu erano più
luminose di quelle gialle, a loro volta più luminose di quelle rosse, con
l’eccezione di alcune stelle dei tipi spettrali G-K-M, di dimensioni molto più
grandi (giganti e supergiganti) ed alcune stelle molto calde , ma di piccole
dimensioni (nane bianche) che non seguivano questo trend, differendo così da
quelle del primo tipo della cd. “sequenza principale”.Le scoperte dei due
astronomi diedero il via alla costruzione di quello che costituisce una pietra
miliare dell’astronomia moderna ed un indispensabile strumento di indagine : il
diagramma chiamato HR,dalle iniziali dei suoi ideatori, che lega la magnitudine
assoluta alla temperatura effettiva delle stelle ed alla classe spettrale.
Uno dei risultati più famosi ed eclatanti
dell’indagine spettroscopica applicata alla cosmologia , diretta conseguenza
delle ricerche in precedenza effettuate, è stata la scoperta epocale di E.
Hubble sul redshift degli spettri delle galassie e sulla espansione
dell’universo, ma un numero notevolissimo di scoperte è stato possibile ed è
ancora oggi possibile solo con l’esame e l’analisi spettrale, che si estende
sempre più a lunghezze d’onda oltre il visibile, nell’IR e nell’UV.
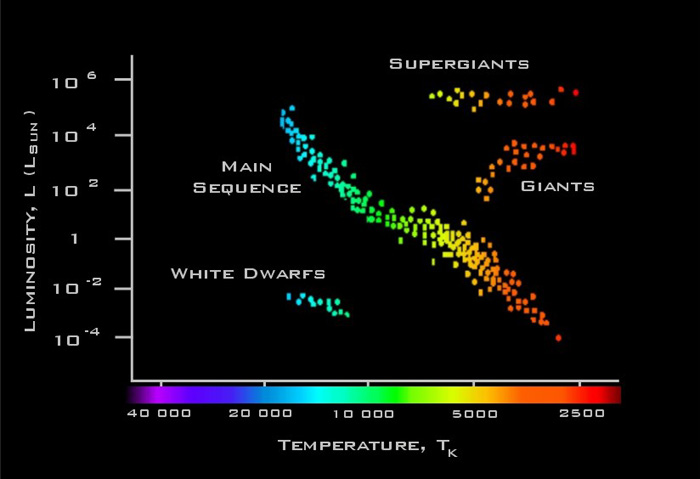
Un esempio del Diagramma HR (Faulkes
Educational Guide)
After Father Angelo Secchi' studies in the field
of stellar spectroscopy, with a classification of stars in 5 categories,
on the basis of their color and the abundance and typology of the lines, the
professional instruments for the spectroscopy greatly improved at the end of 19
th century, with a large amount of lines and details in stellar spectra.The
Harvard College observatory then became the center of a monumental activity of
classification that , thanks to its manager , Edward Pickering, and its
scientists, led to a new classification in 16 classes.Later,(1890) one
scientist of Harvard , Mrs Annie Cannon, simplified the previous
classification bringing it to the one that is familiar to the actual amateur
astronomers, with the letters OBAFGKM.Famous is the rigmarole to remember
the order of classes" Oh, Be A Fine Girl Kiss Me".Mrs Cannon's classification
was a masterpiece of simplicity and efficiency, for the class order was in
the same time a cromatic (and then of temperature) order, and one of complexity
of spectra and their lines, passing from stars of very high temperature and
simple spectra to some with low temperature and very complex spectra.The initial
classification was improved with an under classification, as B0, ..B1..B2,.....A0,...A1...Etc.The
period between the end of 19 th century and the beginning of the 20 th was
the most intense ad fascinating for modern astronomy:Herzsprung and Russel
discovered then that the cromatic order was the brightness order too, buiding
the relation that is considered a milestone of astronomy: the HR diagram.One of
more important and well known results of spectral analisys was the
discovery, by Edwin Hubble, of the galaxies redshift and the expansion of
universe.
Spettroscopia ed astronomia amatoriale
Spectroscopy and Amateur
Astronomy
Il quadro che ho delineato in modo del tutto
sommario e riduttivo è sufficiente per comprendere che senza la spettroscopia la
moderna astronomia ed astrofisica semplicemente non avrebbero potuto esistere:
viene spontanea allora la domanda: C’è un posto per gli appassionati non
professionisti in questa essenziale branca dell’astronomia? La risposta è
affermativa, per entrambe le due grandi articolazioni della spettroscopia:
quella solare e quella stellare.In ciascuna di esse gli astrofili possono
compiere un salto di qualità in termini di conoscenza e comprensione dei
fenomeni che continuamente osservano e riprendono,dando, in alcuni casi anche un
supporto all’analisi professionale (si pensi alla ripresa di spettri di comete e
supernovae).Condizione necessaria per accostarsi a questa splendida realtà e
percepirne appieno la portata è il possesso di uno spettroscopio; molti
astrofili potenzialmente interessati si fermano e desistono nella convinzione
che tale strumento non sia facilmente accessibile, o comunque sia di costo
elevato, e, quel che più conta, sia difficile da usare:nessuna di tali idee è a
mio avviso fondata, come cercherò di dimostrare nelle pagine che seguono.
What I tried to
explain before, in a very simple way, is enough to understand that modern
astronomy and astrophysics could not exist without spectroscopy.Now,
amateur astronomer can make a great step forward in their knowledges in
both the branches : the solar and the stellar spectroscopy.Anyway, a necessary
condition to face this new approach to astronomy is to own a spectroscope: many
amateurs often don't try to enter this new dimension of astronomy for the fear
that this instrument may be of high cost and difficult to use: none of these
thoughts are , in my opinion, true, as I'll try to demonstrate in the
following part of this article.
Cenni
teorici sugli strumenti per la spettroscopia
Theory of instruments for Spectroscopy
a)
La dispersione della luce con un
prisma
Dispersion of light by a prism
La luce
del sole (e di molte altre stelle stelle) è luce bianca e va quindi dispersa in
tutte le sue componenti monocromatiche, dal violetto al rosso.Il modo più
semplice e più usato in passato per ottenere ciò è quello di usare un prisma,
sfruttando il principio della rifrazione, in base al quale quando la luce passa
attraverso un prisma le lunghezze d’onda più lunghe (parte rossa dello spettro)
vengono rifratte in misura diversa e subiscono una deviazione con un angolo
inferiore di quelle più corte (blu-violetto) .Ciascuno di noi ha potuto , almeno
una volta, ammirare la bellezza dei colori della luce solare scomposta nei suoi
colori fondamentali da un oggetto di vetro presente in casa.Il prisma ideale per
ottenere una buona dispersione è un prisma di vetro flint equilatero, con angoli
di 60°, ma anche altri prismi di diversa angolazione possono essere adattati.
Nella Fig 1 è mostrato un esempio di spettro solare ottenibile con un prisma a
60° opportunamente orientato, proiettato su un foglio di carta bianco. Un
prisma può anche essere anteposto ad un obiettivo fotografico agendo quale
prisma –obiettivo per la registrazione di spettri stellari.
Dal
punto di vista dell’indagine spettroscopica, il prisma presenta tuttavia un
serio inconveniente: la dispersione spettrale è piuttosto limitata,come si può
osservare nella Fig 2 dove uno spettro ottenuto con un prisma di vetro flint è
messo a confronto con quello con un reticolo di diffrazione a trasmissione da
300 l/mm.Inoltre , cosa ancora più importante,la dispersione è non lineare, in
quanto proporzionalmente minore nella parte rossa dello spettro rispetto a
quella blu-violetto: lo spettro blu-violetto avrà quindi un’estensione maggiore
di quello rosso: chi abbia un interesse meno che provvisorio per la
spettroscopia non può che rivolgersi ad un altro strumento : il reticolo di
diffrazione.Chi scrive ha usato raramente sistemi a prismi, ritenendo
enormemente più efficienti i sistemi a diffrazione.

Fig1 : Dispersione della luce solare di un prisma:notare
la differente estensione dello spettro blu rispetto al rosso
Dispersion of sun light by a prism:note the different
extension of blue and red spectrum

Fig. 2: Confronto tra la dispersione di un prisma e quella di un reticolo
Comparison between the dispersion of a prism and a 300
g/mm transmission grating
The sunlight (and the light
from many stars) is white light and must be diffracted in all
its monocromatic components, from violet to the red : the simplest
way, and most used in the past to obtain this , is to use a prism, applying
the principle of refraction, on whose basis , when the light passes through a
prism the longer wavelenght (red part of spectrum) are refracted and bear a
deviation with an angle narrower than the shorter wavelenght (blue -
violet part).In the upper image Fig 1 is shown an example of solar
spectrum obtained by a prism.Anyway, using a prism has a noticeable issue:
spectral dispersion is quite less than a grating and not linear, for it's
less in the red part of spectrum respect the blue part .In Fig 2
is shown the dispersion of a prism compared to that of a 300 g/mm transmission
grating; the image speak by itself.
b) La diffrazione con reticolo
Diffraction by a grating
Una
breve premessa sulla natura della diffrazione della luce, sulla quale si basa la
costruzione dei reticoli.La diffrazione è un fenomeno basato sulla stessa natura
ondulatoria della luce e consiste nella deviazione rispetto alla propagazione in
linea retta che un’onda presenta quando incontra un ostacolo: se consideriamo
la diffrazione che avviene col passaggio di un fascio di luce attraverso due
fenditure, esistono regioni dove si crea un interferenza costruttiva, e regioni
dove si crea un interferenza distruttiva.L’interferenza costruttiva avviene ad
angoli diversi a seconda delle diverse lunghezze d’onda (colori).Tale concetto
può esser generalizzato per n fenditure, e le linee o scanalature del reticolo
possono essere assimilate a delle fenditure: maggiore quindi sarà il numero
delle linee per mm del reticolo e maggiore sarà la dispersione che esso, a
parità di altre condizioni, potrà fornire.Si può quindi definire in ultima
analisi il reticolo di diffrazione come
quello strumento capace di trasmettere o
riflettere o (a seconda che sia a trasmissione o a riflessione ) le diverse
lunghezze d’onda di una sorgente di luce policromatica in diversi angoli di
diffrazione. Il fascio di luce incidente su un reticolo è in parte trasmesso o riflesso
(Ordine 0) ed in parte diffratto più volte sia a destra che a sinistra del
raggio stesso, secondo i vari ordini di diffrazione (che non sono altro che i
picchi di energia luminosa diffratta),che prendono numeri negativi e positivi.
L’ordine 1 è quello nel quale il fascio diffratto presenta la maggiore energia
relativa, mentre negli altri man mano questa decresce. l’ordine 1 (ed in
particolare il +1) è lo spettro più luminoso,dove l’energia è maggiore ma anche
quello dove la dispersione è minore rispetto agli ordini inferiori, nei quali
gli spettri sono più elongati. Nei reticoli con un numero medio basso di
linee/mm si verifica il fenomeno della sovrapposizione degli ordini.In
sintesi,accade che la parte rossa dell’ordine 1 si viene a sovrapporre
parzialmente a quella UV dell’ordine 2, lo spettro rosso dell’ordine 2 viene a
sovrapporsi a quello blu dell’ordine 3 e cosi via,”inquinando” l’immagine
spettrale.A tale problema si ovvia, i genere, con l’uso di filtri che isolano la
lunghezza d’onda che si desidera osservare, ovvero con l’uso di reticoli con un
elevato numero di linee/mm (superiore a 1200) in modo da “distanziare” tra loro
gli spettri dei vari ordini ed evitare o ridurre (entro certi limiti ) il
problema.Quanto detto in precedenza impone anche una considerazione; l’ordine
zero, come si è visto, costituisce l’immagine reale dell’oggetto celeste di cui
si vuole osservare lo spettro, sia esso stella , pianeta o sole, quindi occorre
prestare la massima attenzione, specie con i sistemi di spettroscopi senza
fenditura od a fenditura molto aperta,dotati di reticoli a trasmissione, a non
osservare mai l’immagine diretta di ordine 0 del sole.I reticoli oggi più usati
per gli strumenti professionali sono tuttavia quelli a riflessione, e ciò per
una semplice considerazione: nei reticoli a trasmissione la maggior parte
dell’energia luminosa (circa il 60%) è convogliata verso l’ordine 0, ovvero
l’immagine dell’oggetto, e la restante divisa tra i vari ordini.Nei reticoli a
riflessione è, invece possibile,effettuando le incisioni sul
reticolo secondo un certo angolo, detto angolo di “blaze” i convogliare il
massimo dell’energia luminosa, sino anche al 90% su di un solo ordine, e, al suo
interno, in una data lunghezza d'onda, con ovvie
conseguenze positive sull’incisione dell’immagine spettrale .Si dirà quindi che
il reticolo X è "blazed" per 500 nm nell'ordine 1 quando la maggior parte
dell'energia luminosa diffratta verrà diretta verso tale ordine e,
principalmente, verso la zona blu-verde dello spettro di ordine 1.Per ulteriori
riferimenti al processo di blazing nei reticoli a riflessione vedere più avanti
e la fig 3.
A short introduction to the nature of diffraction of
light, which is the basis of gratings.Difraction is based on the behaviour
of light as a wave and is the deviation of a wave from a straight line in presence of an
obstruction on its path: if we consider the diffraction that take place with the
passage of a wave of light through two slits,there exist places were it is
created a constructive interference, and other were we have a destructive one.The
constructive interference take place in different angles, depending on the
wavelenghts (and the colours); such a statement may be extended to n slits, and
the greater the number n, the wider will be the dispersion.We can then define a
grating as
the instrument capable to transmit or
reflect (depending if it is a transmission or reflection one)the different
wavelenghts of a polycromatic source in different diffraction angles.The
light ray that hits a grating is partially transmitted or reflected (0 order)
and partially more times diffracted on its right and left , into the various
diffraction orders,defined by increasing numbers, so we have:
.....-3......-2.....-1 .....0......+1.......+2......+3....... orders the great
the number, the less the relative energy and the more the dispersion.In the low
groove per mm gratings may take place the overlapping of orders, say that the
deep red of 1st order spectrum may overlap the UV- violet part of 2 nd order
spectrum, the red part of order 2 nd spectrum overlaps the blue part of 3
rd order, and so on.This issue is generally fixed using high g/mm gratings and
using filters to select the wavelenght to be studied.The gratings used in
professional instruments are essentially those of reflection type, and this for
the reason that the most of energy in transmission gratings is directed to 0
order (the real image of the object) and the remaining divided between the
various orders.In reflection gratings is , instead, it is possible, by making
the grooves with a certain angle,called "blaze angle", to send the great part of
light energy, till 90%, on a date order and, inside it, on a specified
wavelenght.One say, than, that the grating X is "blazed for 500 nm in the
1st order, when the great part of energy of diffracted light is directed toward
the 1st order spectrum and, inside it, toward the blue - green part of spectrum
itself.For futher informations about the blazing process in the reflection
gratings, see below and the fig 3.
Gli Spettroscopi
The spectroscopes
Possiamo ora parlare degli strumenti per la
spettroscopia ed in particolare della loro autocostruzione.Per comodità mi
riferirò esclusivamente agli spettroscopi a reticolo, dato che quelli a prismi
vengono raramente usati in conseguenza dell’elevato livello di efficienza
raggiunto dai reticoli.Esistono anche spettroscopi nei quali l'elemento
dispersivo è composto da reticoli e prismi (grism), ma la loro costruzione ed il
loro uso è essenzialmente professionale ed esula da questa trattazione.
Gli elementi necessari per la costruzione di uno
spettroscopio amatoriale tipo sono essenzialmente quattro: il reticolo, la fenditura,
l’ottica collimatrice, l’ottica della camera o di osservazione.A questi quattro
elementi fondamentali deve aggiungersi il box contenete il reticolo, col sistema
meccanico di movimentazione del reticolo, ovvero il basculamento dello
stesso sul proprio asse, in modo da poter esplorare tutto lo spettro di un dato ordine.Per
immagini e riferimenti sugli strumenti completi vedere i link del presente sito
sugli strumenti per la spettroscopia, la spettroscopia solare e stellare, e gli
strumenti CLAUS, HIRSS e HIRSS2.
Del
reticolo ho discusso in precedenza: preciso soltanto che
intenderò riferirmi in seguito ai reticoli a riflessione, che sono quelli da me
usati nei miei spettroscopi, passo ora a
parlare della fenditura.
La
fenditura assolve l’importante funzione di costituire l’apertura di entrata
di uno spettroscopio , di garantire l’omogeneità della radiazione in ingresso
che arriva al mezzo di dispersione (prisma o reticolo) per tramite del
collimatore, nonchè di selezionare accuratamente la luce dell'oggetto ripreso od
osservato.Per assolvere in modo ottimale questa funzione è necessario che le
lame della fenditura siano lavorate a tolleranze ottiche, siano perfettamente
parallele, e la loro distanza reciproca sia regolabile, come un diaframma.
Una fenditura professionale che risponda a tutti
questi requisiti avrebbe tuttavia il difetto, per un amatore, di costare
sicuramente di più dell’intero spettroscopio che egli conta di assemblare
(mediamente tra i 300 ed i 1000 €).Occorre
quindi fare di necessità virtù e scendere a qualche compromesso.
Il
primo è l’autocostruzione, ma a tale proposito è bene dire che una fenditura
regolabile, a meno di non avere la disponibilità di una officina meccanica, e di
difficile autocostruzione, mentre una fenditura fissa è relativamente semplice
da assemblare anche in casa.E’ bene, a tale riguardo, sgombrare il campo da un
luogo comune che vuole che le lamette da barba costituiscano l’ideale: le lame
affilate da entrambi i lati non funzionano, in quanto suscettibili di dare
immagini impastate o doppie, è necessario che le lame abbiano un profilo
triangolare con la parte piana rivolta verso la sorgente di luce; ed un oggetto
di uso comune che possieda lame rispondenti a tale requisito è un temperamatite,
anche se con l’ inconveniente di essere generalmente di ferro anziché di
acciaio, e di poter dare origine a ruggine,Si trovano, tuttavia, anche
temperamatite con lame in acciaio, e sono i più adatti.Personalmente ho una vasta provvista
di temperamatite, e spesso, quando vado ad acquistarli, sorrido nel vedere la
faccia meravigliata ed incuriosita del venditore nel vedere che li osservo
controluce per verificare la qualità delle lame: un modo di costruzione di una
fenditura del genere è descritto al link: http://www.lightfrominfinity.org/autocostruzione.htm
.Un’altra possibilità, per le fenditure regolabili, è quella di rivolgersi al
mercato del surplus, dove un rivenditore americano , Surplushed (http://www.surplushed.com),
ne vende alcune ad un prezzo assolutamente conveniente e con un eccellente
rapporto qualità-prezzo.Ritengo queste ultime le più utili per la costruzione di
uno strumento di una certa precisione.Per quanto riguarda il controllo della
fenditura, sia essa autocostruita che acquistata, occorre dire che l’esame delle
lame con un mirino loupe od altro sistema di ingrandimento può essere utile
esclusivamente per verificare il parallelismo delle lame, e non anche la loro
qualità, specie a fenditura molto chiusa; per ottenere ciò è consigliabile
esaminare le frange d’interferenza prodotte dal passaggio attraverso le lame da
un raggio di luce coerente,possibilmente quella di un laser, meglio se a luce
verde.Più queste sono dritte, ben delineate e regolarmente spaziate, più la
fenditura è adatta per l’uso cui è destinata.
L’0ttica di collimazione o collimatore è
l’elemento di uno spettroscopio la cui funzione è di rendere parallelo il fascio
ottico da inviare al reticolo, ossia di collimarlo.In pratica si tratta (se
costituito da sistemi a lenti) di un
cannocchiale sistemato all’incontrario, il cui obiettivo è rivolto verso il
reticolo e sul cui focheggiatore è alloggiata la fenditura: è necessario inoltre
che quest’ultima sia posta esattamente sul fuoco dell’obiettivo.In prima
approssimazione, per verificare ciò, si può controllare visualmente l’incisione
delle lame traguardate attraverso l’obiettivo, ma per un posizionamento preciso
è necessario poi, una volta assemblato lo spettroscopio, focheggiare l’immagine
dello spettro prima grossolanamente con l’obiettivo della camera e poi
spostando solo la fenditura sino a che le righe non risulteranno le più
nette possibili.La lunghezza focale del collimatore è connessa a quella
dell’ottica di osservazione o della camera, nel senso che in genere si opta per
rapporti 1:1 rapporti diversi a favore dell’ottica di osservazione (tipo 2 o 3 a
1) avrebbero l’effetto ingrandire eccessivamente l’immagine (ossia le righe)
senza alcun guadagno nella risoluzione spettrale, che è invece dato dal numero
di righe per mm del reticolo e dalle sue dimensioni: la scelta della focale del
collimatore dipenderà quindi dalla finalità di utilizzo dello strumento, per
il sole o per le stelle, per l’alta o la bassa risoluzione.Per il sole è in
genere preferibile usare focali medie o lunghe, data l’enorme quantità di luce
in arrivo ed il notevolissimo numero di righe ( oltre 8700) osservabili, per le
stelle e con telescopi commerciali è bene invece tenersi su focali basse, anche
per ottenere una scala immagine che comprenda la maggior parte dello spettro da
osservare . Il diametro del collimatore dovrà coprire e preferibilmente essere
leggermente superiore alla diagonale del reticolo (che si ottiene moltiplicando
il lato per 1,4, nel caso di reticolo quadrato).Se, quindi, come è probabile,
acquisteremo un reticolo quadrato da 30 mm , sarà necessario avere un
collimatore di D > 42 mm.
L’ottica di osservazione ha la funzione
di ingrandire il fascio parallelo diffratto proveniente dal reticolo, ossia lo
spettro, ed osservarlo tramite un oculare o riprenderlo con una camera CCD,
webcam, digicam o quant’altro.Il diametro dovrebbe essere pari alla diagonale
del reticolo, od anche poco inferiore, mentre la lunghezza focale sarebbe
opportuno fosse pari o al massimo leggermente superiore a quella del
collimatore.
Inutile dire che gli obiettivi fotografici e
quelli (ma non tutti) per fotocopia, facilmente rinvenibili questi ultimi, nei
mercatini o rivenditori di surplus , costituiscono eccellenti ottiche, sia di
collimazione che della camera,per il campo piano che forniscono.La focale
dovrebbe aggirarsi, per spettroscopi a risoluzione bassa e media, tra i 50 e 150
mm.
Un
discorso a parte merita il BOX contenente il reticolo la cui struttura è
in funzione del progetto di spettroscopio, se solare, stellare o di uso
universale, e dell’ordine spettrale che si intende osservare con quel tipo di
reticolo. Cerco di spiegarmi: se si intendono osservare spettri stellari , o, ad
esempio, lo spettro solare nell’IR od in una data riga a risoluzioni elevate, e
quindi l’intensità della radiazione in ingresso nello spettroscopio gioca un
ruolo fondamentale, allora è necessario utilizzare l’ordine +1 (quello più
luminoso) e quindi prevedere un angolo di circa 38° tra collimatore ed ottica
della camera.Nel caso di spettroscopi solari a medio- alta risoluzione ed in
tutti i casi in cui si intenda avvalersi di una maggiore risoluzione spettrale
(spettri più estesi) al prezzo di una minore luminosità degli stessi, allora può
essere utilizzato l' ordine -1,od ordini superiori al 1° che
hanno una minore luminosità, ma il vantaggio di una maggiore dispersione con un
angolo elevato che rende pratico un box con attacchi a 90°.Un modo piuttosto semplice e valido di realizzare un box è quello di
tagliare un quadratino di alluminio 6 x 6 cm o 8 x 8 cm da 2 o 3 mm di spessore
facendo ricavare dei fori filettati del diametro necessario (o filettati 42 x 1) su due delle facce a
90° per applicarvici le ottiche di collimazione ed osservazione, realizzando poi dei tappi laterali
di chiusura che possono anche essere di PVC.Personalmente ho utilizzato tale soluzione in parecchi dei miei
spettroscopi.
The
spectroscopes
I'll talk about of instruments for
spectroscopy, and particularly of their self making:I'll talk about grating
spectroscopes, the most used by amateurs.For any further information about
spectroscopes, see the link to this site about instruments for spectroscopy,
solar and stellar spectroscopy, and the CLAUS, HIRSS, HIRSS 2 spectroscopes.The component of an amateur
spectroscope are essentially four:The grating, the slit, the collimating optics,
the camera or observation optics. It is to be considered another one, the box
containing the grating and its movement system around its own axis. I discussed
before about the
grating, I
want only underline that , in following chat, I'll refer exclusively
to reflection grating. I'll talk now of the
slit.
The slit
is the entrance opening of a spectroscope, and it
assure the homogeneity of radiation to be sent to the grating by means of the
collimator.To do in the best way its job, it's necessary for the jaws of the
slit to be worked at optical tolerances, say to be" diffraction
limited", to be exactly parallel to each other, and to be adjustable in their
distance .A professional slit with all (or part) of these features would have
the problem of an high cost.A good adjustable slit may cost between 400- 1000 $,
surely more than the cost of the whole spectroscope.It is then necessary to try
to make it by ourselves, or to find cheap ones.In order to the first approach,
it is necessary to underline that the razor blades, commonly thought to can be
used as slit, doesn't work, for they are sharpened on both sides,
with a "V" shape , and give unsharp or doubled images of spectrum lines.An
object of common use we can fit as a slit is a pencil sharpener, because its
blades are sharpened on one side only and have a triangle shaped profile: anyway, it will be useful to find one in
stainless steel, to avoid rust.The sharpened side is to be directed toward the
grating, an the plane side to the object.The assembling of such a device is
described at the link:http://www.lightfrominfinity.org/autocostruzione.htm
.The surplus seller Surplushed in USA has some
unexpensive adjustable slits in its catalogue, good to begin.
The collimation optics or collimator
It is the component of a spectroscope whose task
is to make parallel the rays coming from the slit and sent to the
grating.It is , in a few word, a refractor telescope (if a lens system)
set at the contrary, with the objective lens toward the grating and the focuser
toward the slit: it's necessary, furthermore, that its objective is exactly
focused onto the slit: to obtain this, one can observe the slit jaws through the
lens and vary the distance until they look sharp.Anyway, this approach is the
first to do, and , after assembled the spectroscope, it's necessary a fine
focusing, first of the camera objective and after without moving
anything else, of the collimator lens, until the lines will appear very
sharp.Generally, the focal lenght of collimator ought in general to be the same
of the camera lens (1:1 ratio) every increase in this ratio (1:2 and so on) for
example a collimator of 100 mm and a camera lens of 200, will magnify the
spectrum image without a real gain in spectral resolution.For the sun it will be
useful a medium FL collimator, for the great flux of light entering it, for,
the stars it's useful to take FL lower.The collimator objective will fully light
up
the grating, so it will be in diameter not minor than the grating's diagonal.
The observation or camera optics
It has the function to enlarge the diffracted parallel
light beam caming from the grating, say the spectrum, and observe it by means of
an eyepiece or taking a picture of it by a CCD camera, a digicam, webcam, and so
on.The diameter ought to be equal, or greater, to the grating diagonal.
It's useful to remember short focus that camera lens
and copy objectives (say 50-150 mm) are often the best choice to act both as
collimator and observation optics.
The grating Box
Its structure is strictly connected to the project of
the spectroscope to be made.If one intend to build a stellar spectroscope, then
is necessary to use the order +1, where the intensity of diffracted light is
higher and consequently an angle of about 38° between collimator and
observation optics.If we like to study the solar spectrum, then we can take
advantage from the use of the higher orders, where the intensity is less (but
this is not influent in the case of the sun), but the dispersion is quite
stronger.A simple way to realize a box is to use an aluminum square barrel
6 x 6 or 8 x 8 cm, and to make a threaded 42 x 1 hole on two of its faces
(to connect to the collimator and observation optics) and two plastic caps on
the free sides.
Box 1
La radiazione elettromagnetica
The
electromagnetic radiation
Radiazione
Lunghezza d’onda
Onde radio
Radio Waves > 10
cm
Microonde
Microwaves
10 cm – 1
mm
Infrarossi Infrared 1 mm – 700 nm
Luce visibile Visible
700
nm
– 400 nm
Ultravioletti
UV 400 nm – 10 nm
Raggi X X
Rays
10 nm – 1
pm
Raggi
gamma Gamma Rays < 1 pm
L’occhio umano riesce a
percepire la radiazione visibile da 400 a 700 nm circa (1nm = 1/1.000.000
mm = 10 Angstrom
The uman eye intercepts the visible radiation from 400 to 700 nm about (1nm
= 1/1.000.000 mm = 10 Angstroms
I sensori CCD vanno ben
oltre, essendo in grado di registrare la radiazione incidente da 350 nm (UV)
a 1000 nm (IR) seppure con diverse intensità a seconda dei
sensori.
CCD Sensors go far beyond these limits, with a
registratio of incoming radiation from 350 nm (UV) till 1000 nm (IR), but
with different intensities depending on the sensors.
Box 2
Il Corpo Nero
The Blackbody
Il corpo nero è per
definizione un corpo capace di assorbire tutta la radiazione
elettromagnetica, sia nel visibile che nelle altre regioni dello spettro
(IR, UV ) senza rifletterne.Il suo nome deriva dalla circostanza che, ove illuminato con una
luce di qualsiasi lunghezza d’onda esso la assorbe tutta.
Il corpo nero è quindi
un’astrazione , un modello di riferimento, che non esiste in realtà e che ha
senso solo se esistono corpi reali (tra cui le stelle) ad esso assimilabili.Il
concetto che esso sottende è necessario in quanto, sussistendo un legame
diretto tra lo spettro emesso da un corpo nero e la sua temperatura sulla base
delle leggi di Planck, di Stefan- Boltzman e di Wien, e potendosi quindi
determinare la sua temperatura attraverso lo spettro, è possibile applicare
lo stesso principio anche alle stelle.
Blackbody
is defined a body capable to absorb all the incoming electromagnetic
radiation both in visible and other spectral regions as UV and IR.It is
then an abstraction. in the sense that it doesn't exist , but exist some
real bodies, like stars, quite similar to it.This concept is necessary on
the basis of relation between spectrum of a blackbody and its temperature
for Planck, Stefan Bolzman and Wien Laws, and if we can obtain its
temperature on the basis of its spectrum, we can apply the same principle to
the stars.
Alcune
ulteriori
considerazioni sui reticoli di diffrazione:dal
reticolo allo spettroscopio
Some further considerations about
diffraction gratings: from the grating
to the spectroscope
Premetto di non essere un
teorico, men che mai in un campo come quello della fisica nel quale le mie
conoscenze sono state acquisite da autodidatta .Sento spesso parlare,
nell’ambito della spettroscopia, di risoluzione e dispersione spettrale, range
spettrale, risoluzione lineare etc, con dovizia di formule matematiche ed
assunti teorici che spesso creano non poca confusione nei non addetti ai
lavori.
Ritengo quindi di fare cosa
utile cercando di semplificare al massimo la questione riportando solo le
formule essenziali ,a mio beneficio ed a
quello di altri, in modo che anche l’astrofilo senza una laurea in astronomia o
fisica possa comprendere alcuni concetti base dei reticoli di
diffrazione,componenti principali dei moderni spettroscopi, e degli spettroscopi
stessi.Parlerò solo dei reticoli, in quanto ritengo personalmente l'uso dei
prismi superato dalla evoluzione e disponibilità dei primi, nettamente superiori
quanto a potere dispersivo.
Innanzitutto, una breve
definizione di reticolo:
Definirei
reticolo di
diffrazione quello strumento capace di riflettere o trasmettere (a seconda che
sia a riflessione od a trasmissione) le diverse lunghezze d’onda di una sorgente
di luce policromatica in diversi angoli di diffrazione.
Il reticolo permette quindi
di ottenere luce monocromatica da una sorgente policromatica o di luce bianca.Naturalmente
lo spettro in uscita da un reticolo è formato da diversi colori, ma se si
evidenzia una parte soltanto di tale spettro, grazie, ad esempio ad una
fenditura in uscita, si ottiene luce monocromatica.Un
esempio del funzionamento di un reticolo a riflessione semplice è quello
riportato in fig 2B, si può ossservare la scomposizione dello spettro nei vari
ordini , a destra e sinistra dell'ordine 0 (per comodità sono riportati solo i
primi) ed il fatto che lo spettro di ordine 0 non è altro che la riflessione del
raggio incidente.
Esistono due tipi
fondamentali di reticoli a riflessione, uno denominato reticolo inciso (“Ruled diffraction
grating”) che consiste di un substrato di vetro ottico alluminato sul quale
vengono incise, con un apposito strumento a punta di diamante un gran numero di
righe equidistanti : tali incisioni, angolate, vengono effettuate in modo tale
da concentrare il massimo dell’energia luminosa in un dato angolo e quindi in
una determinata lunghezza d’onda: in reticolo si dice allora “blazed” per quella
data lunghezza d’onda.La lunghezza d’onda di “blaze” è quindi quella dove il
reticolo ha la massima efficienza.Di tali reticoli vengono messe in vendita
repliche dell'originale, di prezzo all'incirca 1/10 dell'originale stesso. A tale riguardo è necessaria una precisazione:
aumentando il numero degli ordini, diminuisce dello stesso rapporto l’efficienza
del reticolo nell’angolo di blaze per cui e stato prodotto: vale a dire che un
reticolo che è stato “blazed” per 5000 A nel 1° ordine sarà blazed, cioè avrà il
picco di efficienza a 2500 A nel 2° ordine.In parole povere, se voglio
investigare, ad es. il tripletto del Magnesio a 5167 A nel 2° ordine, per
avvantaggiarmi di una maggiore dispersione, allora dovrò procurarmi un reticolo blazed per 10000 A nel 1° ordine oppure
per 5000 A nel 2° ordine.Tale avvertenza è
necessaria in quanto gli angoli di blaze pubblicizzati dalle case produttrici si
riferiscono in genere al 1° ordine.Tuttavia, occorre anche tener conto delle
modalità costruttive dei reticoli e delle relative curve di efficienza, che
spesso differiscono a seconda delle modalità costruttive e per i materiali
usati.Per una migliore comprensione del processo di blazing
nei reticoli a riflessione si può osservare la
fig 3:come si può osservare, in pratica il blazing è il processo in base al quale si angolano le
incisioni di un reticolo, in modo da ottenere una nuova normale, non più
perpendicolare al
substrato, ma al piano angolato dell'incisione,in modo che la posizione di
massima intensità, prima corrispondente al raggio riflesso di ordine n = 0, è
spostata verso una nuova riflessione, B, anch'essa = 0, nella direzione nella
quale il raggio incidente avrebbe dovuto essere riflesso sulla base delle leggi
dell'ottica geometrica.Ciò comporta una maggiore energia luminosa del segnale
diffratto nella zona spettrale corrispondente a quella per la quale è
stato calcolato l'angolo di blaze.
Il secondo tipo è denominato
“olografico” (“Holographic diffraction grating”) nel quale le righe sono
ottenute con tecniche olografiche, con l’uso di lasers, e nei quali le relative
incisioni sono di apparenza smussata, sinusoidale.Possono essere "blazed" solo
con speciali procedimenti , che ne fa lievitare notevolmente il costo, per
contro possiedono meno luce diffusa dei reticoli "ruled".
Esistono anche reticoli di
diffrazione concavi (“Concave diffraction grating”) essi sono ricavati su un
substrato di vetro ottico concavo, che quindi ha una focale.In questo modo tali
reticoli hanno una molteplice funzione, in quanto fungono sia da elemento
dispersivo che da collimatore ed ottica di osservazione nello stesso tempo.La
loro caratteristica è che mettono a fuoco su un cerchio, detto cerchio di
Rowland, a seconda della lunghezza d’onda.Essi sono in genere ottenuti con
procedimenti olografici.La controindicazione è il loro costo, che è elevato.Il
sottoscritto è venuto fortunosamente in possesso di uno di essi, estratto da uno
spettrometro di massa acquistato d’occasione in un mercatino, ed è rimasto
stupito dalla versatilità di un simile reticolo, che da solo, con una fenditura
ed un oculare, permette di osservare spettri solari di eccellente qualità (vedi
lo spettroscopio COGOS nel link “ spettroscopia solare).Il loro costo è tuttavia
molto elevato (un reticolo concavo da 25 mm costa circa 700 €).
Oltre ai tipi suddetti
esiste infine, e si riporta solo per notizia, una categoria di reticoli detti
"Echelle Gratings", di utilizzo
limitato all'ambito professionale, che permettono l'uso degli ordini di numero
più alto, quelli a maggiore dispersione, che nei reticoli normali presentano un
angolo troppo elevato per essere utilizzabili, e che , essendo sovrapposti l'uno
all'altro vengono separati da un secondo elemento dispersore posto a croce
col primo.
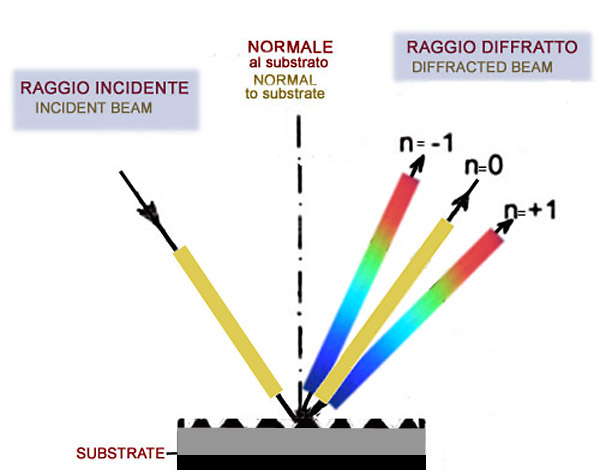
Fig 2B Dimostrazione del funzionamento di un reticolo a riflessione
How a reflection diffraction grating works
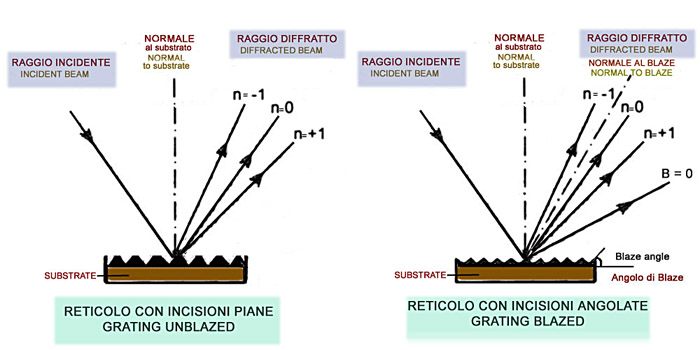
Fig 3 : Differenza tra reticoli a riflessione blazed e non blazed
Difference between blazed and unblazed reflection gratings
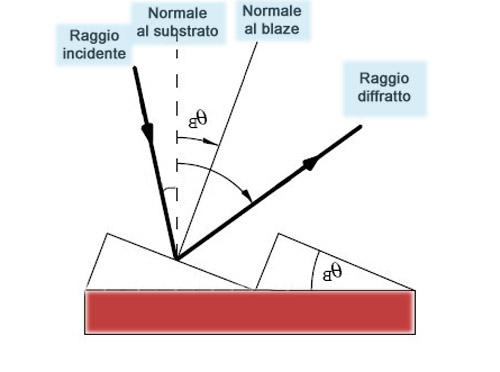
Fig 4 : Particolare del
blazing
Blazing
detail
L’equazione base del
reticolo è:
(sen a +
sen b) = N x M x y x 10^- 6
dove:
a = Angolo del raggio
incidente in gradi
b = Angolo del raggio diffratto
in gradi
M = Ordine di diffrazione
N = Densità di righe per mm.
y = lunghezza d'onda
in nanometri
1nm =
(10)^- 6= 1/1000000 mm
Dalla predetta uguaglianza
appare che: 1) a e b sono misurati rispetto alla perpendicolare (linea normale)
al reticolo, 2) a parità di densità di righe per mm, M x y è una costante, e , quindi, che, aumentando
l’ordine M, y (la lunghezza d’onda) dimezzerà, pur essendo presente.Ciò comporta,
oltre alla conseguenza precedentemente accennata circa l’angolo di blaze del
reticolo, anche quella che , ad una data lunghezza d’onda e quindi ad un dato
angolo di diffrazione, vi può essere la sovrapposizione di più ordini,ossia la
sovrapposizione di più spettri. Ad esempio, all’angolo corrispondente a
8000 A (800nm) nel 1° ordine, saranno altresì presenti le lunghezze d’onda di 4000 A per
il 2° ordine, di 2666 A nel 3° ordine, e 2000A per il 4°.Ciò spiega perché, per
dati reticoli e date lunghezze d’onda, sia necessario interporre dei filtri per
far passare soltanto la lunghezza d’onda desiderata ed evitare “annacquamenti”
dell’immagine spettrale.
I’m not a theorist, especially in a field as physics, in
which my knowledges were obtained by myself.I often hear to talk, in the
spectroscopy questions, of spectral range, spectral dispersion, spectral
resolution, and so on, with abundance of mathematical formulas, often different
from each other, that are confusing for the people without a physics or
astronomy degree.
I intend, then, try to simplify some basic concepts of
diffraction gratings, main components of modern spectroscopes and of
spectroscopes itself, in order to make them intelligible to every kind of
reader.I'll talk about gratings only, for I think the of prisms no
longer useful for amateur spectroscopy for the low dispersion, while there
is a great availability, on the market, of medium priced good
gratings.
First of all, a brief definition of grating:
We
should define a diffraction grating as that device capable
of spreading (reflecting or trasmitting) the different wavelengths of a polychromatic light source in
different angles.
The grating is then able to display, from a polycromatic,
white source, a monochromatic one.The spectra obtained by such a device is, of
course, spread in different colours, but , if we put a slit in exit of the
diffracted beam, we’re able to see only monochromatic light of different
wavelengths.Fig 2B shows how works a simple
reflection grating .
There are three main types of reflection diffraction gratings:
the Ruled diffraction gratings, that consist of a glass
substrate carrying a layer of deposited aluminium that has been ruled with a
large number of equidistant grooves, using a diamond-edge tool.The grooves are
ruled in a proper angle, to concentrate most of light energy in a specific
wavelength.They’re told to be “blazed” for that wavelength, called the “blaze”
wavelength, where the grating is most efficient These gratings are
usually available in "replicas" of the original, to get a lower cost, generally
1/10 than the first.Here is necessary to make a
consideration: the blaze wavelength of a grating becomes lower as the spectral
order increases, so, a grating blazed, for example at 5000 A in the first order
is blazed for 2500 A in the second.Then, if I want to observe, maybe, the
Magnesium triplet at 5167 A in the second order, I’ll need a 10000A blazed in
the first order grating, or a 5000A blazed in the second one.The maximum
efficiency for each of higher orders decreases as the order increases.It is
necessary, anyway, to take in account the efficiency curves of gratings, that
often differ from theoretical ones in relation to the materials being used and
to the production’s systems.For a better understanding of the blazing process
see the fig.3, where we can observe that in practice blazing consist in angling
the surface of grooves so that the original maximum intensity n = 0 spectrum is
shifted in another position b = 0 , rendering the higher orders brighter.
The Holographic diffraction grating, in which the grooves are
produced using holographic techniques, by mean of lasers.The grooves, in this
case, aren’t “angle” shaped, but have a smooth, sinusoidal shape. This type of
grating can be "blazed", bust the cost is high.They show, anyway, less
stray light then the ruled gratings.
The
Concave
holographic gratings
that accomplish the task of two optical elements, the
diffracting and the focusing one, in a single component: it has a great
efficiency, but the price is high.I was able to get one from a mass
spectrometer bought in a surplus market and was astonished of how good it was to
do the job of a home made spectroscope with the only help of a slit and an
eyepiece (see COGOS spectroscope in the link solar spectroscopy).They can be
blazed too, but the cost is very high: a 25 mm grating may cost up to 700 €.
Another type of grating, used only in professional
instruments, is the "Echelle grating"
which are capable to use very high orders whose
dispersion is the best, and that in normal gratings are not visible, or
visible at very small angles and superimposed to each other.Spectra of
such orders need, for observing, to be separated with another dispersive
element, mounted crossed with the echelle.
The basic equation of a grating is the following:
(sin a + sin b ) = N x M x y
x 10^- 6
where :
a = Incoming ray angle
in degrees
b = Diffracted ray angle
in degrees
M = Diffraction order
(integer)
N = Groove density per mm
y = Wavelenght in
Nanometers
1nm =
(10)^- 6= 1/1000000 mm
From that equation it is evident that : 1) a and b are
measured in relation to the "normal" line (perpendicular) to the grating
substrate 2)
for the same groove
density, M x y is a constant, an then, increasing the order M, the wavelength will
halve, and , for example, at the location of 8000 A (800nm) in the first order, the
wavelengths of 4000 for the second order, 2666 for the third, 2000 for the
fourth will also be present.The consequence
is that, if you want to see only
the 1st order spectra, you must use a filter to eliminate the
higher orders.
1- Risoluzione spettrale di un reticolo
La
risoluzione spettrale di un reticolo è data dalla separazione tra due picchi
spettrali individuabili come separati dallo
strumento : conviene ora, per
maggior precisione, tener
conto dei dati in Angstrom.
R = M x N x P
E, relativamente ad una data
lunghezza d’onda:
R = Y/ M x N x P
Dove:
-
R = potere risolutivo
-
M = ordine di diffrazione
-
N = numero di righe per mm
-
P = dimensioni del reticolo in mm.
-
Y = Lunghezza d’onda interessata in Angstrom
Un reticolo di 1200 l/mm di
30 mm di lato, avrà quindi una risoluzione di 36000 nell'ordine 1
e,a 5000 A una risoluzione di: 5000/
1200 x 30 = 5000/36000 = 0,14 A.
Nell’ordine 2 la
risoluzione, sempre a 5000 A sarà: 5000/1200 x 30 x 2= 5000/ 72000 = 0,07 A
ossia in pratica
raddoppierà.
1-
Grating Spectral resolution
Spectral resolution of a grating can be defined as the
separation between two spectral peaks shown separated by the device.
The related equations are the following:
R = M x N x P
And, in relation to a fixed wavelength:
R = Y/ M x N x P
Where:
-
R =
Resolving power
-
M =
Diffraction order
-
N =
Number of grooves per mm
-
P =
Grating dimensions in mm
-
Y =
Interested wavelength in A
Then, a 1200 g/mm grating, 30 mm sided, will get, in the 1 st
order a resolution of 36000 and,, at 5000 A , a resolution of 5000/1200 x 30 = 0.14 A
In the 2nd order the theoretical resolution will
be: 5000/1200 x 30 x 2= 0.07 A , doubled.
Il reticolo, tuttavia, non è
un elemento a sè stante, ma va utilizzato, in spettroscopia, insieme ad altri
componenti.E’ un pò, se mi si può perdonare la forzatura, simile ad un obiettivo
astronomico: un obiettivo da 60 mm, ad es., ha un potere risolutivo teorico di 2
sec. d’arco, ad esempio, ma tale potere risolutivo, per essere sfruttato a
pieno, necessita di altri elementi, oculari, camere di ripresa, tubo ottico, etc,
ognuno dei quali ha la sua importanza.Immaginiamo cosa può succedere ad un
ottimo obiettivo con un oculare pessimo, o con un tubo non in asse.
Tornando alla spettroscopia,
il potere risolutivo del sistema non è dato solo dal reticolo, ma anche da altri
elementi, le ottiche di collimazione e di osservazione, e la fenditura, dove
questa è presente.
Cercherò quindi di
procedere con l’accostamento precedente, anche se improprio:
Immaginiamo le ottiche di
uno spettroscopio simili agli oculari di un telescopio, la cui lunghezza focale
determina la capacità di raggiungere o meno (a parte discorsi di qualità) il
potere risolutivo teorico dell’obiettivo, solo che qui le cose sono invertite:
mentre con gli oculari, quelli a focale più corta consento di risolvere più
particolari, qui è l’inverso, più lunga è la focale delle ottiche, più aumenta
la capacità dello strumento di raggiungere o migliorare, entro certi limiti, il
potere risolutivo teorico del reticolo.Per quanto riguarda la fenditura avviene
il contrario rispetto alle ottiche, e, a somiglianza degli oculari, più piccola
è la sua apertura, più elevato sarà il potere risolutivo del sistema.
Veniamo quindi ad un'altra
relazione interessante ai nostri fini:
2) Dispersione di un
reticolo
La dispersione angolare di
un reticolo ad una data lunghezza d'onda è data dal rapporto dell’ammontare del cambiamento dell’angolo di
diffrazione in corrispondenza ad un dato cambiamento differenziale della lunghezza d’onda
stessa.
Essa vale, considerando la
simbologia sopraindicata:
db/dy =
M x N x 10^-7/ cos b
La dispersione lineare,
sempre in Angstrom, è data dal prodotto della dispersione angolare per la focale
delle ottiche applicate al reticolo e vale, considerando F la focale:
f x db/dy
= F x M x N x 10^ -7/cos b
= F x M x N / (10)7 x
cos b =
F x M x N / 10000000
cos b
Essa è un indicatore
particolarmente importante negli spettroscopi in quanto definisce l’estensione
dell’intervallo spettrale alla fenditura di uscita dello strumento, ed è
associata alla capacità del medesimo di risolvere fini particolari spettrali ed
è espressa in mm/A, mentre quella inversa , più comoda ed usata, è
espressa in A (o nm) / mm:
10000000 x
cos b / F x M x N
Ad esempio, quindi, un
reticolo da 1200 l/mm, con un angolo di diffrazione di 10° a 5000 A, al quale sono state
applicate ottiche di 200 mm di focale(sia come collimatore che della
camera) ha, nell'ordine 1, una dispersione lineare pari a:
10000000 x cos 10 / 200 x 1
x 1200 = 40 A/mm
E' facile vedere che
nell'ordine 2 tale dispersione raddoppia e diventa 20 A/mm.
A questo punto occorre fare
un'altra interessante precisazione: la dispersione lineare indicata è calcolata
per un mm: ora, se la fenditura d'ingresso dello spettroscopio è chiusa a valori
inferiori a questo la dispersione cambia in proporzione e da la risoluzione
effettiva del sistema: quindi, nel caso
precedente, il valore di dispersione lineare, per una fenditura chiusa a 1/10 mm
diventa 4 A/mm e 2 nel 2° ordine, se chiusa a 1/20 mm 2 A/mm ed 1 nel 2° ordine
, e così via .Ovviamente chiudendo la
fenditura la luce che arriva all'oculare od alla camera si riduce e di questo
occorre tener conto.
The
grating, anyway, isn't a device to use "stand alone" but is generally the
main component of spectroscopes, and is to be used with other elements that have
a great importance too.It's something alike, maybe, an astronomical objective:
such objective, for example a 60 mm, has a 2 arcsecs resolving power, but that
theoretical power, to come real, needs that all others elements of the telescope,
tube,eyepiece, diaphragms, and so on are properly installed and of good
quality.Imagine a good objective in a curved tube, or with a low quality
eyepiece.I want to say that the resolving power and the image quality of a
spectroscope depend not only on the quality and the type of grating, but also on
the optics and the slit, if there's one,been used .
Let's
imagine, now, the grating as an astronomical objective, apart any consideration
on the quality, the lower the focal lenght of the eyepiece, the higher the
chance to observe at the theoretical resolution: there's, if I remember well, a
magnification called "resolving magnification", that is equal to half objective
diameter in mm.For spectroscopes is the contrary: the higher the FL of the
optics, the higher the resolving power of the system and the chance to use all
the grating's quality and resolving power, and, on the side of slit, the
narrower its aperture, the higher the resolving power of the system.
Let's
go to see, now an interesting relation:
2 -Grating dispersion
The
dispersion of a grating may be angular if it defines the quantity of change of
the diffraction angle corresponding to a small change in the wavelenght:
db/dy =
M x N x 10^-7/ cos b
Linear
dispersion is the product of this term and the effective focal lenght of the
system:
f x db/dy
= F x M x N x 10^ -7/cos b
= F x M x N / 10^7 x
cos b =
F x M x N / 10000000
cos b
It is
a very important indicator in the spectroscopes for it defines the extention of
spectral interval at exit slit (or eyepiece) and it's stricyly connected to the
ability to show the spectral details.It's usually showed in mm/A, but the one
most used is the inverse A/mm that's the reciprocal of previous relation:
10000000 x
cos b / F x M x N
For
example, then, a diffraction grating of 1200 g/mm, with a diffraction angle of
10°at 5000A,to which have been applied 200 mm FL optics, has in the 1st order, a linear
dispersion of:
10000000 x cos 10 / 200 x 1
x 1200 = 40 A/mm
It's
easy to see that, in the second order, it becomes 20 A/mm.
At
this point it's useful to underline that the result of such a relation is for 1
mm, and it is strictly dependent on the slit opening, determining the
effective
system resolution; as I said before, if the
slit is shut, maybe, at 1/10 mm, the result becomes 4 A in the first order
and 2 in the second.Obviously, the narrower the slit, the higher linear
dispersion and resolving power, but the lower the incoming light on the exit
slit , the eyepiece, or the camera.
3)
Dispersione lineare su un CCD
Per ottenere la dispersione
lineare inversa misurata su un CCD basta moltiplicare la relazione precedente per la
grandezza dei Pixel in mm, e sarà espressa in A/pixel:
Sarà quindi
P =
G x 10000000 x
cos b / F x M x N
Dove:
P = Dispersione lineare di
un CCD
G = Grandezza dei pixel in
mm
b = angolo di diffrazione
F = focale delle ottiche
M = ordine
N = numero di linee per mm
del reticolo.
Nell'esempio precedente, nel
caso il CCD abbia pixel di 10 micron, ossia 0,010 mm si ha che la dispersione
del CCD cui è stato applicato il sistema descritto, reticolo ed ottiche, vale:
0,01 x 10000000 x 0,98 /
200x1x1200 = 98000/ 240000 = 0,4 A/ pixel
La risoluzione effettiva del
sistema spettroscopio, chiudendo la fenditura a 1/10 di mm diventa quindi,
misurata dalla camera, di 0,4 / 0,1 = 0,04 A/pixel e così via.Naturalmente
occorre anche tener conto della modalità di acquisizione dell'immagine; ad es,
una camera con i pixel da 10 micron,se usata in binning 2 x 2 raddoppierà le
dimensioni dei pixel, che dovranno essere considerati pari a 20 micron.
3) Linear Dispersion onto a CCD camera
To
obtain the linear dispersion on a chip of a CCD camera, it's enough to multiply
the previous relation for dimensions of pixel in mm.It will be measured in
A/Pixel.
P =
G x 10000000 x
cos b / F x M x N
Where
P =
Linear dispersion on a CCD
G =
Pixel dimensions in
mm
b =
Diffraction angle
F =
Optics FL
M =
Order
N =
Number of grooves per mm of the grating
In the
previous example, in the case of a CCD with 10 micron pixel, we 'll have:
0,01 x 10000000 x 0,98 /
200x1x1200 = 98000/ 240000 = 0.4 A/ pixel
The
effective resolution of the spectroscope system will be, if we shut down the
slit opening at 1/10 mm, 0.4 / 0.1 = 0.04 a/pixel, and so on.Of course, it
is necessary to consider also the image acquisition mode: in case of
a binning 2x2, the pixel dimensions will be doubled, and, in the example, it
will be of 20 micron.
Possiamo quindi dire, in
ultima analisi, che il potere risolutivo del sistema spettroscopio , come
costituito dai suoi tre componenti fondamentali: reticolo, ottiche fenditura (o
fenditure, nel caso ve ne siano due, in ingresso ed in uscita) e camera di
ripresa dipende, a parità di lunghezza d’onda , di dimensioni del reticolo e di
ordine, da quattro fattori fondamentali: il n° di linee per mm del reticolo, la
focale delle ottiche, l'ampiezza della fenditura e la dimensione dei pixel della
camera CCD.Dei quattro, il fattore che
presenta meno limiti fisici, potendo essere facilmente essere raddoppiato, a
pena solo della portatilità del tutto, sono le ottiche.Passare da 500 a 1000 mm
o da 1000 a 3000 è relativamente facile, spesso se si usano sistemi ottici
aggiuntivi quali barlow o duplicatori di focale. Passare, invece, da un reticolo
ruled replica da 600 a 1200, può essere ancora agevole , ma da 1200 a 2400, ad
es., potrebbero sorgere problemi, in quanto tali reticoli sono spesso
ottimizzati per l’UV vicino.Chiudere la fenditura oltre pochi centesimi di mm
potrebbe comportare, specie nel caso di fenditure fatte in casa o non lavorate a
tolleranze ottiche,un peggioramento dell'immagine complessiva.Anche il raddoppio dei pixel della camera, anche se
talvolta possibile, potrebbe risultare molto dispendioso: passare da una camera,
come la Philips Vesta o Toucam , con sensori da 5,6 micron e dal costo di un
centinaio di € potrebbe voler dire acquistare una ben più costosa camera con
pixel, ad es. da 2,5 – 3 micron.
In definitiva, quindi, a mio
parere, il sistema immediato e più economico per raddoppiare il potere risolutivo
del sistema è quello di raddoppiare la focale delle ottiche con l’uso di
duplicatori di focali e lenti di barlow.Nel mio spettroscopio solare COGOS, come
si è visto, l’uso di tali dispositivi ha permesso di passare da una risoluzione
di 0,23 A/Pixel a 0,08 A/pixel in pratica senza aumenti avvertibili delle
dimensioni dello strumento.
Relativamente alle ottiche,
occorre ancora fare alcune precisazioni:
1- Il collimatore dovrà
avere un obiettivo con un diametro tale da coprire la diagonale del reticolo, e
quindi almeno pari a 1,4 il lato di questo.
2 – L’obiettivo del
telescopio della camera dovrà avere almeno lo stesso diametro di quello del
collimatore.
3 – Le due ottiche dovrebbero
anche avere la stessa focale, tuttavia, nel caso così non sia, è sempre
opportuno che quella della camera, per l’osservazione dell’immagine della
fenditura con lo spettro in uscita dal reticolo, sia di focale superiore a
quella del collimatore, ciò perché l’ingrandimento complessivo dello
spettroscopio è dato dal rapporto F camera / F collimatore.
Un discorso a parte vale la
possibilità di utilizzare, nel caso di strumenti solari, un terzo telescopio
avente la funzione di inviare un immagine del sole sulla fenditura d’ingresso
dello spettroscopio.Cio per : a) avere lo spettro non della “luce solare”, ma
del disco solare e di
una parte specifica (macchie, flares,) etc della fotosfera o della cromosfera,
b) una immagine composita dell’apparenza del sole ad una data lunghezza d’onda
(Ha, calcio, Hb, sodio, elio, etc) nel caso si disponga di un sistema di
sintetizzazione delle immagini applicato alle fenditure, in ingresso ed in
uscita: il relativo strumento prende il nome di spettroelioscopio.Esempi di
spettroelioscopi , pur funzionanti in modo digitale e non meccanico, sono
forniti da HIRSS e HIRSS 2, la cui trattazione è negli appositi link del sito.
We can say,then , that the resolving power of spectroscope
system, as formed by its main components: grating, optics, slit (or slits, in
the case there are two) and CCD camera depends, for the same wavelength, grating
dimension and order, on three fatctors: grating’s density, optics, and pixel’s
dimension, and the relation is linear, crescent , so, the bigger one of those
factors will be, the larger will be the system’s resolution.Among these factors,
the one more easily to be doubled, with a little lost in portability is the
optics’ focal length: to go from , say, 1000 mm to 2000 will be easy
accomplished by the use of a barlow lens, while going from a 1200 g/mm ruled
replica grating to a 2400 one should be more difficult for, may be, the ruling
of this for the near UV, and so on.
The doubling of camera’s pixels should also be expensive:
think to a passage from an inexpensive camera as a Philips Vesta or Toucam ,
with a 5,6 micron pixel chip to a better, but much more expensive CCD cameras
with 3 micron pixel chip.
In my opinion, the most useful way to double the
spectroscope’s resolution is to double the optics’ FL by using Barlow lens or
photo teleconverters.This was the way I used in COGOS spectroscope to pass from
a 0,23 A/pixel to a 0,08 A/pixel resolution.
About spectroscope optics it’s useful to underline the
following points:
1-The collimator lens must have a diameter to cover the
grating’s diagonal: it will be 1,4 times the side of this.
2 – The camera lens must have at least the same diameter as
the collimator lens.
3 – The two optics (collimator and camera) should have the
same focal length: anyway, in case this isn’t possible, it’s better that the
camera optics have a longer fl than the collimator lens, as the overall
magnification of the instrument is given by the ratio Camera FL / Collimator FL.
A separate topic is the use of a third telescope , with the
function to send a solar image onto the entrance slit of the spectroscope, in
order to get not the simple “solar light” spectra, but the one of some features
of sun photosphere or cromosphere (sunspots, flares, etc.), or, in other cases,
a composite image of the sun in a given wavelength (Ha, Calcium, Hb, Helium, and
so on).Such instrument is called spectrohelioscope.Some examples of
spectrohelioscopes, but acting in digital mode, are my HIRSS and HIRSS 2
instruments, whose details are shown in the links of this website.
 ->2
->2






